Geometría en la vida cotidiana

El estudio de esta rama de la matemática es uno de los más antiguos y aun en la actualidad seguimos usando la geometría en la vida cotidiana. A lo largo de los años se ha desarrollado gracias al trabajo de importantes personajes como Euclides, Apolonio, Rene Descartes, Pitágoras, entre otros.

¿Cómo es usada la geometría en la vida cotidiana?

Desde muy temprana edad estamos familiarizados con los conceptos básicos que estudia esta ciencia, como puntos, rectas, planos y espacios, así como las relaciones elementales que existen entre ellos. Estas mismas nos permiten relacionar el espacio y las figuras que forman parte de la realidad en la cual nos desenvolvemos como puertas, ventanas, pelotas, entre otros.

Formas geométricas en la vida cotidiana

Estas nociones básicas aparentemente muy elementales, son en realidad muy complejas por su elevado nivel de abstracción, la necesidad de la enseñanza de la geometría corresponde, en primer lugar, al papel que esta desempeña en la vida diaria.

Actualmente es imposible no ver la geometría en la vida cotidiana, puesto que está presente en muchos ámbitos como la arquitectura, mecánica, geografía, astronomía, ingeniería, diseño industrial, etc.

Algunos usos de la geometría en la vida cotidiana

Geometría en la ingeniería

En la ingeniería civil la aplicación de esta rama de la matemática esta en el diseño y análisis de ciertas estructuras que soportan cargas, como lo son edificios, puentes, maquinas, entre otros.

Geometría en la astronomía

Podemos ver que la geometría está muy vinculada a ella, por el hecho de que en todo el universo predominan las formas geométricas, como las orbitas de los planetas en torno a una estrella. Al principio la astronomía ha tomado ciertos elementos de la geometría para poder sustentar ciertas cosas, como las coordenadas que son vitales para que los astrónomos puedan situar objetos en la bóveda celeste.

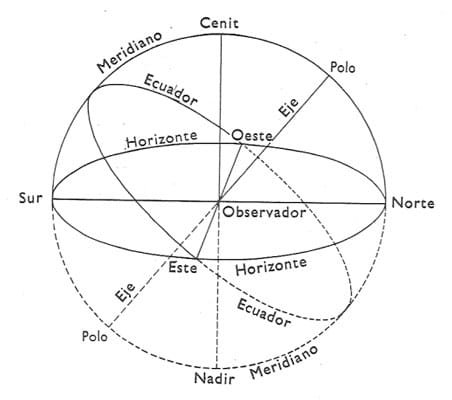Geometría en la Esfera celeste

Geometría en las artes plásticas

A nivel artístico también se han utilizados los conceptos y figuras geométricas, muchos artistas hacen uso de estos conocimientos para sus representaciones plásticas, entre ellos se destacan Wassily Kandinsky, Piet Mondrian y Alejandro Otero.

Por otra parte, los diseñadores gráficos hacen uso de la geometría en la vida cotidiana, estos la aplican en sus trabajos o creaciones el uso de un determinado objeto que pueda transmitir una idea directa, como por ejemplo: un cuadrado puede transmitir solides y fortaleza, o un círculo puede representar un ciclo, este también es sinónimo de protección, movimiento y adaptabilidad.

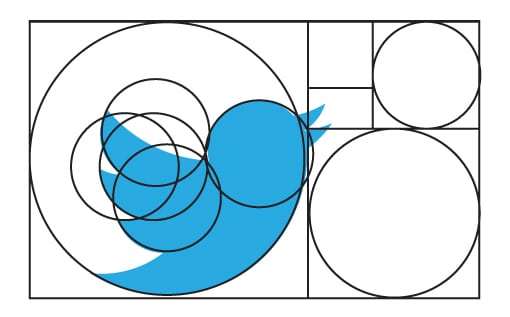Logo de Twitter creado con formas geométricas

¿Es importante la geometría en la vida cotidiana?

Como podemos ver la geometría no es solo una rama de la matemática que estudia rectas, puntos y segmentos, es mucho más que eso. Puesto que tiene grandes aplicaciones en otras ciencias y en cuanto nos desenvolvemos en nuestra vida diaria, e incluso en el lenguaje utilizado comúnmente.

VIDEO SOBRE EL TEMA, PARA MAYOR COMPRENCION DEL MISMO: