LA PROBABILIDAD

Qué es la probabilidad

Una de las características más especiales de los seres humanos, que nos diferencia del resto de animales, es nuestra capacidad de “predicción”, de anticiparnos a los acontecimientos que van a ocurrir. A veces fallamos, pero otras muchas no. Esta capacidad nos ha permitido llegar hasta donde estamos hoy, pudiendo predecir tanto peligros como oportunidades. Piénsalo, nuestros antepasado que eran capaces de predecir el ataque de un depredador fueron los que sobrevivieron. Ahora, decenas de miles de años después hemos dado un paso más y nos preguntamos ¿Qué es la probabilidad?

La probabilidad es el cálculo matemático que evalúa las posibilidades que existen de que una cosa suceda cuando interviene el azar.

Vamos a plantear un par de ejemplos, porque la probabilidad -como tantos conceptos en matemáticas, es una construcción abstracta, pero con ejemplos se entiende mejor.

Si giras la siguiente ruleta, ¿en qué números se puede parar?

La ruleta se puede parar en un número del uno al cinco. Hemos construido, sin darnos cuenta, lo que se llama un experimento (girar una ruleta) y el espacio muestral (los números del uno al cinco). El espacio muestral es un conjunto que tiene por elementos los sucesos que se pueden dar, esto es, los números del uno al cinco.

Por nuestras experiencias en el mundo de los juegos ya sabemos más cosas del experimento anterior. Es posible que la ruleta se pare en uno de esos números y es imposible que salga un ocho, por ejemplo. ¡Sabemos un montón de probabilidad y no nos dábamos cuenta!

Vamos a plantear otro experimento, en otro contexto distinto:

Viendo este aparcamiento, si sale un coche de los que están aparcados, ¿de qué color podría ser?

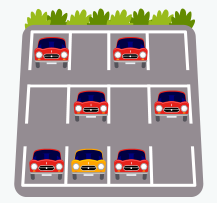
Las posibilidades están muy claras, del aparcamiento podría salir un coche rojo o un coche amarillo. Es imposible que salga un coche verde, o una moto azul. Pero, aunque es posible que salga un coche amarillo, hay mucha más probabilidad de que sea rojo, porque hay muchos más coches rojos que amarillos.

Cómo se calcula la probabilidad

Para calcular la probabilidad, continuando con el ejemplo anterior, no hay más que contar los coches que hay de cada color. Como 6 de los 7 coches del aparcamiento son rojos, podemos plantearlo como una fracción: la probabilidad de que del aparcamiento salga un coche rojo será una fracción con numerador 6 (el número de coches rojos) y denominador 7 (el número total de coches).

La probabilidad de que salga un coche rojo sería igual a 6\7. La probabilidad de que salga un coche amarillo sería igual a 1\7. La probabilidad de que salga un coche azul sería 0, porque no hay coches azules aparcados.

Generalizando esta idea llegamos a cómo se calcula la probabilidad: con una fracción que se suele llamar regla de Laplace. Ponemos en el numerador el número de casos favorables y en el denominador el número de casos posibles.

Ya podemos calcular probabilidades de sucesos sencillos. Por ejemplo, podemos hacer predicciones de las bolas que pueden salir de este bombo:

En el bombo hay 8 bolas:

• La probabilidad de que salga una concreta de él es 1\8

• Pero cuatro bolas son iguales, y tienen el número 5, por lo que la probabilidad de que salga un cinco es 4\8. Si te piden que apuestes por algún resultado, el más probable es el cinco.

Ejemplo: Lanzar una moneda al aire

Si lanzas una moneda la probabilidad de que salga cara es 1\2 , fíjate que es la misma de que salga cruz.

Ejemplo: Tirar un dado

Si lanzas un dado de seis caras la probabilidad de que salga un tres será 1\6 .

También puedes calcular la probabilidad de que salga un número par, ya que las caras que muestran un número par son 3 (2, 4 y 6) de un total de seis caras, es, por tanto, = 3\6=1\3

Para qué sirve la probabilidad

La probabilidad se utiliza en muchas áreas como las matemáticas, la estadística, la física, la economía, las ciencias sociales, entre otras. Los primeros estudios de probabilidad se desarrollaron para resolver problemas de juegos y es allí dónde más se nota su uso, porque te puede servir para tener más oportunidades de ganar, o para ahorrarnos dinero (al no jugar a juegos en los que es muy probable perder).

Ejemplo pares y nones

Fíjate el siguiente ejemplo vinculado al juego infantil de Pares y nones.

Pares y nones es un juego que se utiliza para elegir entre dos personas a una de las dos. Dos personas eligen entre par o impar, y sacan a la vez un número de dedos de una mano que tenían detrás de la espalda. En función de que la suma de los dedos que hayan sacado sea par o impar se elegirá al que eligió esa opción.

La sorpresa, si has jugado alguna vez a pares y nones, es que no es igual de probable que salga una opción o la otra, no es como lanzar una moneda al aire, no es un juego justo. La probabilidad demuestra que hay más posibilidades de que salga un número par que uno impar.

Puedes verlo en esta tabla, donde están marcados los números pares en amarillo. Si te fijas hay 25 resultados posibles y 13 de ellos son números pares.

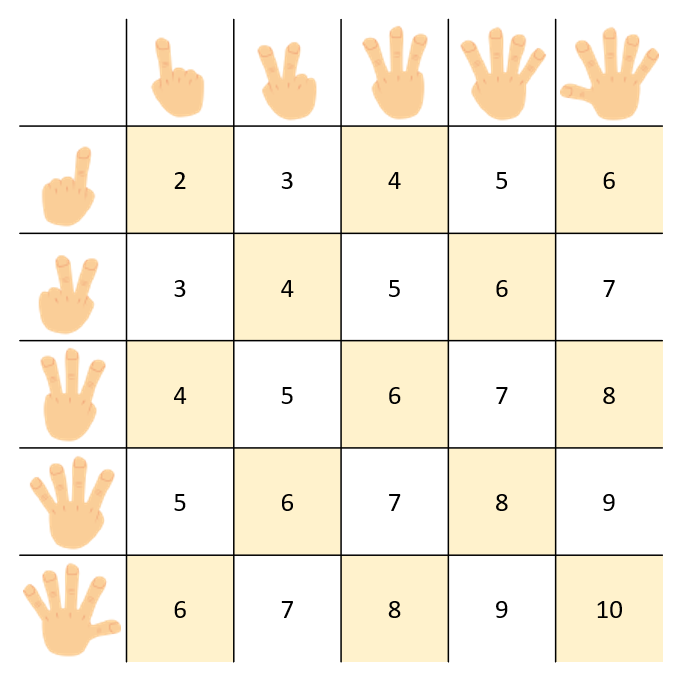
La diferencia es pequeña, pero si juegas “pares” tienes un 4% más de probabilidad de ganar, ya que 13\25=0.52, mientras que 12125=0.48.

Ejemplo Lotería de Navidad

Si crees que un 4% es muy poco, te sugiero que no compres lotería ya que la probabilidad de que salga en número de los cien mil que hay en el bombo es 1\100000=0,00001, un diminuto 0,001%. Ese número es aproximadamente el mismo que el de elegir una gota de agua correcta en un bidón de cinco litros.

Pero no todos los sucesos dependen de la probabilidad, muchos están condicionados por otros factores.

video para su mayor comprensión a continuación: